个人随笔
目录
图的存储结构之邻接矩阵和邻接表（Java实现）
2020-04-21 23:51:07

一、图的存储结构讨论

对于线性表来说，是一对一的关系，所以用数组或者链表均可以简单存放。
对于树结构是一对多的关系，所以我们要将数组和链表的特性结合在一起才能更好的存放。
对于图来说，是多对多的情况，另外图上的任意一个顶点都可以被看做是第一个顶点，任一顶点的邻接点之间也不存在次序关系

如下图：实际是一个图结构，只不过顶点位置不同。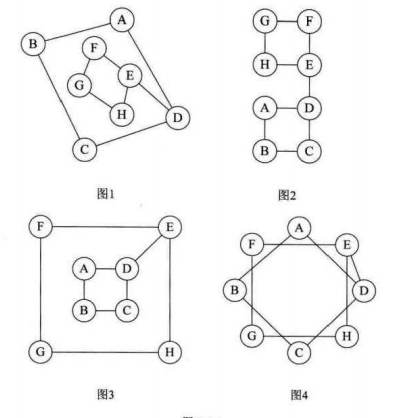

由于图的结构复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在内存中的物理位置来表示元素之间的关系，也就是说，图不可能用简单的顺序存储结构来表示。内存物理位置是线性的，图的元素关系是平面的。

虽然我们可以向树结构中说到的那样使用多重链表，但是我们需要先确定最大的度，然后按照这个度最大的顶点设计结点结构，若是每个顶点的度数相差较大，就会造成大量的存储单元浪费。

二、图的存储结构（1）—-邻接矩阵

考虑到图是由顶点和边（弧）两部分组成的，合在一起是比较困难的，那就很自然的考虑到分为两个结构来分别存储

顶点因为不区分大小，主次，所以用一个一维数组来存储时不错的选择。

而边或弧由于是顶点与顶点之间的关系，所以我们最好使用二维数组来存储，图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

1、无向图

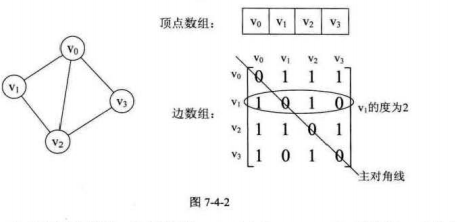
  1. 其中1表示两个顶点之间存在关系，0表示无关，不存在顶点间的边。

对称矩阵：就是n阶矩阵满足a[i][j]=a[j][i](0<=i,j<=n）。即从矩阵的左上角到右下角的主对角线为轴，右上角的源与左下角相对应的元都是相等的。

根据这个矩阵，我们可以很容易的知道图中的信息。

  • 1.我们要判定容易两顶点是否有边无边就非常容易了。
  • 2.我们要知道某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行（或第i列）的元素之和。比如上图顶点v1的度就是1+0+1+0=2
  • 3.求顶点vi的所有邻接点就是将矩阵第i行元素扫描一遍，arc[i][j]为1就是邻接点

2、有向图

对于上面的无向图，二维对称矩阵似乎浪费了一半的空间。若是存放有向图，会更大程度利用起来空间

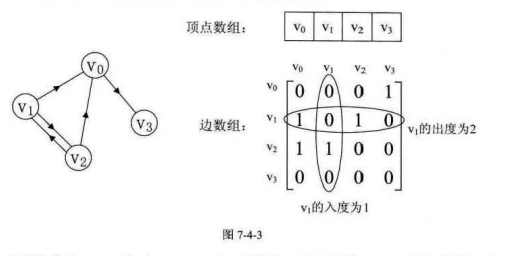
其中顶点数组是一样的和无向图，弧数组也是一个矩阵，但因为是有向图，所以这个矩阵并不对称：例如v1->v0有弧，arc[1][0]=1,而v0到v1没有弧，所以arc[0][1]=0。

另外有向图，要考虑入度和出度，顶点v1的入度为1，正好是第v1列的各数之和，顶点v1的出度为2，正好是第v2行的各数之和

3、网

每条边上带有权的有向图就叫做网

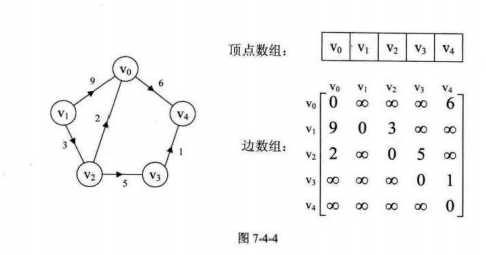
这里‘∞’表示一个计算机允许的，大于所有边上权值的值

4、Java实现无向图、有向图、网的邻接矩阵创建

  1. public class G2 {
  3.     public static void main(String[] args) {
  4.         //1、无向图
  5.         //定点数组vertex
  6.         String[] v1 = new String[]{"V0","V1","V2","V3"};
  7.         //矩阵表示边的关系edge 其中1表示两个顶点之间存在关系，0表示无关，不存在顶点间的边。
  8.         int[][] e1 = new int[][] {
  9.             {0,1,1,1},
  10.             {1,0,1,0},
  11.             {1,1,0,1},
  12.             {1,0,1,0}
  13.         };
  14.         System.out.println("输出无向图：");
  15.         for (int i = 0; i < v1.length; i++) {
  16.             System.out.print(v1[i]+"\t");
  17.         }
  18.         System.out.println();
  19.         for (int i = 0; i < v1.length; i++) {
  20.             for (int j = 0; j < v1.length; j++) {
  21.                 System.out.print(e1[i][j]+"\t");
  22.             }
  23.             System.out.println();
  24.         }
  26.         System.out.println("--------------------");
  27.         //2、有向图
  28.         String[] v2 =new String[]{"V0","V1","V2","V3"};
  29.         int[][] e2 = new int[][] {
  30.             {0,0,0,1},
  31.             {1,0,1,0},//V1的出度为2
  32.             {1,1,0,0},//V2的出度为2
  33.             {0,0,0,0}
  34.             //V1的入度为1
  35.         };
  36.         System.out.println("输出有向图：");
  37.         for (int i = 0; i < v2.length; i++) {
  38.             System.out.print(v2[i]+"\t");
  39.         }
  40.         System.out.println();
  41.         for (int i = 0; i < v2.length; i++) {
  42.             for (int j = 0; j < v2.length; j++) {
  43.                 System.out.print(e2[i][j]+"\t");
  44.             }
  45.             System.out.println();
  46.         }
  48.         System.out.println("--------------------");
  50.         //3、网，每条边上带有权的图就叫做网
  51.         String[] v3 =new String[]{"V0","V1","V2","V3","V4"};
  52.         //m表示不可达
  53.         int m=65535;
  54.         int[][] e3 = new int[][] {
  55.             {0,m,m,m,6},
  56.             {9,0,3,m,m},
  57.             {2,m,0,5,m},
  58.             {m,m,m,0,1},
  59.             {m,m,m,m,0}
  60.         };
  61.         System.out.println("输出网：");
  62.         for (int i = 0; i < v3.length; i++) {
  63.             System.out.print(v3[i]+"\t");
  64.         }
  65.         System.out.println();
  66.         for (int i = 0; i < v3.length; i++) {
  67.             for (int j = 0; j < v3.length; j++) {
  68.                 System.out.print(e3[i][j]+"\t");
  69.             }
  70.             System.out.println();
  71.         }
  73.     }
  75. }

代码中的图跟上面说的图一一对应，运行结果如下：

  1. 输出无向图：
  2. V0    V1    V2    V3    
  3. 0    1    1    1    
  4. 1    0    1    0    
  5. 1    1    0    1    
  6. 1    0    1    0    
  7. --------------------
  8. 输出有向图：
  9. V0    V1    V2    V3    
  10. 0    0    0    1    
  11. 1    0    1    0    
  12. 1    1    0    0    
  13. 0    0    0    0    
  14. --------------------
  15. 输出网：
  16. V0    V1    V2    V3    V4    
  17. 0    65535    65535    65535    6    
  18. 9    0    3    65535    65535    
  19. 2    65535    0    5    65535    
  20. 65535    65535    65535    0    1    
  21. 65535    65535    65535    65535    0

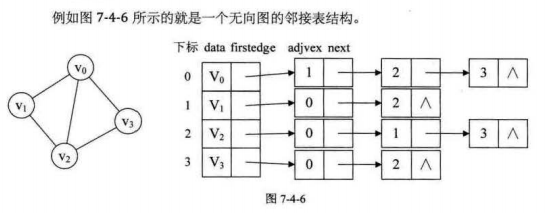
三、图的存储结构（2）—-邻接表

上面的邻接矩阵是一种不错的图存储结构，便于理解，但是当我们的边数相对于顶点较少的图，这种结构是存在对存储空间的极大的浪费。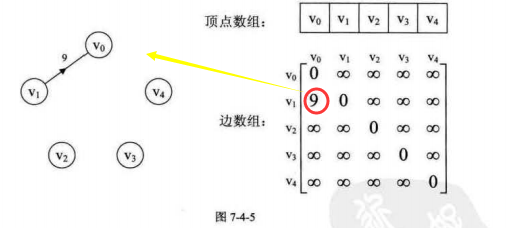

我们可以考虑使用链表来动态分配空间，避免使用数组一次分配而造成空间浪费问题。

同树中，孩子表示法，我们将结点存放入数组，对结点的孩子进行链式存储，不管有多少孩子，都不会存在空间浪费。这种思路也适用于图的存储。我们把这种数组与链表相结合的存储方法称为邻接表。

邻接表处理办法

  • 1.图中顶点用一个一维数组。当然，顶点也可以用单链表来存储，不过数组可以较容易的读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息

  • 2.图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表

    1、无向图


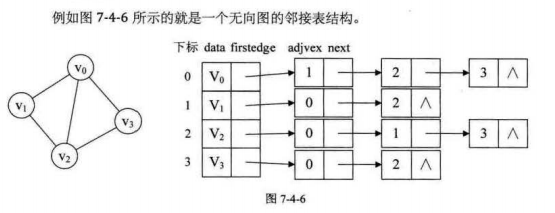
    这样的结构，对于我们要获得图的相关信息也是很方便。比如：
    我们要获取某个顶点的度，就要去查找这个顶点的边表中结点的个数。
    我们要判断vi到vj是否存在边，只需要测试vi的边表链表中是否存在结点vj的下标j即可。
    我们若是要获取顶点的所有邻接点，就是对此顶点的边表进行遍历。

2、有向图

有向图由于有方向，我们是以顶点为弧尾来存储边表的，这样很容易就可以得到每个顶点的出度。但是由于有时也需要确定顶点的入度或以顶点作为弧头的弧，我们可以建立一个有向图的逆邻接表，即对每个顶点vi都建立一个链接为vi为弧头的表。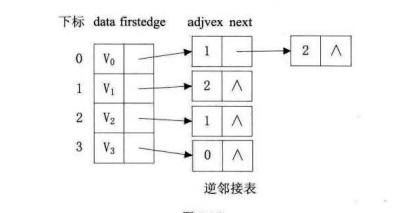

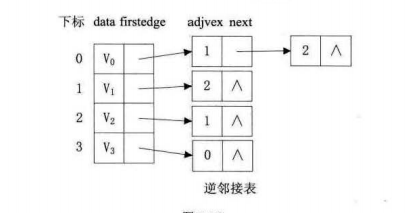
3、带权值的网

们可以在边表结点定义中再增加一个weight数据域，存储权值信息即可。

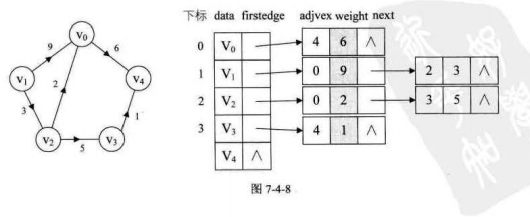
4、Java实现无向图、有向图、网的邻接链表创建

首先我们看一下《算法导论》中关于图的邻接表的定义：图G=(V,E)的邻接表表示有一个包含 |V| 个列表的数组Adj所组成，其中每个列表对应于V中的一个顶点，对于每一个u∈V，邻接表Adj[u]包含所有满足条件（u，v）∈E的顶点v，亦即，Adj[u]包含图G中所有和顶点u相邻的顶点。（或者他也可能指向这些顶点的指针），每个邻接表中的顶点一般以任意的顺序存储。（注意一下这句话！）

这里的实现方法有多重多样，下面是按我的思路实现的代码示例，一般都会有两个对象，一个是顶点，如下：

  1. //定义定点
  2. class Vertex{
  3.     String value;//顶点的值
  4.     Edge firstEdge;//第一条边
  5.     public Vertex(String value, Edge firstEdge) {
  6.         super();
  7.         this.value = value;
  8.         this.firstEdge = firstEdge;
  9.     }
  10. }

这里我们可已将顶点放在一个数组中，然后每个顶点都从第一条边衍生出去。当然可以按具体需求多加属性，比如顶点的出度也可以当做一个属性什么的，我这里就不加了！

然后定义边的对象：

  1. class Edge{
  2.     String value;//该边对应的顶点
  3.     int weight;//权重，无向图，有向图权重为0
  4.     Edge next;//下一个边
  6.     /**
  7.      * 构建一条边 weight未0表示无向图或者有向图 不为0表示网
  8.      * @param value
  9.      * @param weight
  10.      * @param next
  11.      */
  12.     public Edge(String value, int weight, Edge next) {
  13.         super();
  14.         this.value = value;
  15.         this.weight = weight;
  16.         this.next = next;
  17.     }
  18. }

我这里因为要举无向图，有向图，网的例子，所以这个边就直接有权重，但是无向图，有向图的权重为0。

然后下面是完整的代码，跟上面三个示例图对应：

  1. /**
  2.  * 邻接链表
  3.  * @author suibibk.com
  4.  */
  5. public class Graph {
  6.     public int num;//顶点个数
  7.     //顶点
  8.     List<Vertex> vertexs;
  10.     public Graph(int num) {
  11.         this.num = num;
  12.         //初始化图的大小
  13.         vertexs = new ArrayList<Vertex>(num);
  14.     }
  15.     //插入顶点
  16.     public void addVertex(String value) {
  17.         vertexs.add(new Vertex(value, null));
  18.     }
  19.     //获取顶点
  20.     public Vertex getVertex(String value) {
  21.         for (int i = 0; i < num; i++) {
  22.             if(vertexs.get(i).value.equals(value)) {
  23.                 return vertexs.get(i);
  24.             }
  25.         }
  26.         return null;
  27.     }
  29.     /**
  30.      * 添加无向图的边
  31.      * @param vertex1 第一个顶点
  32.      * @param vertex2 第二个顶点
  33.      */
  34.     public void addUndigraphEdge(String vertex1,String vertex2) {
  35.         //因为是无向图，所以就直接加入
  36.         addEdgeByVertex(vertex1,vertex2,0);
  37.         addEdgeByVertex(vertex2,vertex1,0);
  38.     }
  40.     /**
  41.      * 添加有向图的边
  42.      * @param start 开始节点
  43.      * @param end 结束节点
  44.      */
  45.     public void addDigraphEdge(String start,String end) {
  46.         //因为是有向图，所以只有一条边
  47.         addEdgeByVertex(start,end,0);
  48.     }
  49.     /**
  50.      * 添加网的边
  51.      * @param start 开始节点
  52.      * @param end 结束节点
  53.      * @param weight 权重
  54.      */
  55.     public void addWebEdge(String start,String end,int weight) {
  56.         //网就是有向图有权重
  57.         addEdgeByVertex(start,end,weight);
  58.     }
  60.     /**
  61.      * 添加一条由start-->end的边
  62.      * @param start
  63.      * @param end
  64.      * @param weight 权重未0表示无向图或者有向图，部位0表示网
  65.      */
  66.     private void addEdgeByVertex(String start,String end,int weight) {
  67.         //1、找到第一个顶点
  68.         Vertex v1 = this.getVertex(start);
  69.         //2、检查这条边是否已经存在，已经存在就直接报错
  70.         Edge firstEdge = v1.firstEdge;
  71.         while(firstEdge!=null) {
  72.             //获取这个边
  73.             String value = firstEdge.value;
  74.             if(end.equals(value)) {
  75.                 System.out.println("边"+start+"-->"+end+"已经加入，不可以再加入");
  76.                 return;
  77.             }else {
  78.                 Edge next = firstEdge.next;
  79.                 firstEdge=next;
  80.             }
  81.         }
  83.         //到这里就可以加入这一条边了
  84.         firstEdge = v1.firstEdge;
  85.         //到这里就可以加入这条边
  86.         if(firstEdge==null) {
  87.             firstEdge = new Edge(end,weight, null);
  88.             v1.firstEdge=firstEdge;
  89.         }else {
  90.             //当前节点变为第一个节点
  91.             Edge nowEdge = new Edge(end,weight, null);
  92.             v1.firstEdge=nowEdge;
  93.             nowEdge.next=firstEdge;
  94.         }
  95.     }
  97.     /**
  98.      * 输出图
  99.      */
  100.     public void print() {
  101.         for (int i = 0; i <num; i++) {
  102.             Vertex vertex = vertexs.get(i);
  103.             System.out.print(vertex.value+"-->");
  104.             Edge edge = vertex.firstEdge;
  105.             while(edge!=null) {
  106.                 System.out.print(edge.value+"["+edge.weight+"]");
  107.                 Edge next = edge.next;
  108.                 edge=next;
  109.                 if(next!=null) {
  110.                     System.out.print("-->");
  111.                 }else {
  112.                     System.out.print("-->∧");
  113.                 }
  114.             }
  115.             System.out.println();
  116.         }
  118.     }
  120.     public static void main(String[] args) {
  121.         //测试无向图
  122.         Graph g = new Graph(4);
  123.         g.addVertex("V0");
  124.         g.addVertex("V1");
  125.         g.addVertex("V2");
  126.         g.addVertex("V3");
  128.         //插入边:无向图
  129.         g.addUndigraphEdge("V0", "V1");
  130.         g.addUndigraphEdge("V1", "V2");
  131.         g.addUndigraphEdge("V2", "V3");
  132.         g.addUndigraphEdge("V3", "V0");
  133.         g.addUndigraphEdge("V2", "V0");
  135.         System.out.println("输出无向图：");
  137.         g.print();
  139.         System.out.println("------------");
  140.         Graph g1 = new Graph(4);
  141.         g1.addVertex("V0");
  142.         g1.addVertex("V1");
  143.         g1.addVertex("V2");
  144.         g1.addVertex("V3");
  146.         //插入边:有向图
  147.         g1.addDigraphEdge("V0", "V3");
  148.         g1.addDigraphEdge("V1", "V0");
  149.         g1.addDigraphEdge("V1", "V2");
  150.         g1.addDigraphEdge("V2", "V0");
  151.         g1.addDigraphEdge("V2", "V1");
  153.         System.out.println("输出有向图：");
  154.         g1.print();
  156.         System.out.println("----------");
  157.         Graph g2 = new Graph(4);
  158.         g2.addVertex("V0");
  159.         g2.addVertex("V1");
  160.         g2.addVertex("V2");
  161.         g2.addVertex("V3");
  163.         //插入边:有向图
  164.         g2.addWebEdge("V0", "V4",6);
  165.         g2.addWebEdge("V1", "V0",9);
  166.         g2.addWebEdge("V1", "V2",3);
  167.         g2.addWebEdge("V2", "V0",2);
  168.         g2.addWebEdge("V2", "V3",5);
  169.         g2.addWebEdge("V3", "V4",1);
  171.         System.out.println("输出带权值的网：");
  172.         g2.print();
  173.     }
  175. }
  177. //定义定点
  178. class Vertex{
  179.     String value;//顶点的值
  180.     Edge firstEdge;//第一条边
  181.     public Vertex(String value, Edge firstEdge) {
  182.         super();
  183.         this.value = value;
  184.         this.firstEdge = firstEdge;
  185.     }
  187. }
  188. class Edge{
  189.     String value;//该边对应的顶点
  190.     int weight;//权重，无向图，有向图权重为0
  191.     Edge next;//下一个边
  193.     /**
  194.      * 构建一条边 weight未0表示无向图或者有向图 不为0表示网
  195.      * @param value
  196.      * @param weight
  197.      * @param next
  198.      */
  199.     public Edge(String value, int weight, Edge next) {
  200.         super();
  201.         this.value = value;
  202.         this.weight = weight;
  203.         this.next = next;
  204.     }
  205. }

Copy即可运行，结果如下：

  1. 输出无向图：
  2. V0-->V2[0]-->V3[0]-->V1[0]-->∧
  3. V1-->V2[0]-->V0[0]-->∧
  4. V2-->V0[0]-->V3[0]-->V1[0]-->∧
  5. V3-->V0[0]-->V2[0]-->∧
  6. ------------
  7. 输出有向图：
  8. V0-->V3[0]-->∧
  9. V1-->V2[0]-->V0[0]-->∧
  10. V2-->V1[0]-->V0[0]-->∧
  11. V3-->
  12. ----------
  13. 输出带权值的网：
  14. V0-->V4[6]-->∧
  15. V1-->V2[3]-->V0[9]-->∧
  16. V2-->V3[5]-->V0[2]-->∧
  17. V3-->V4[1]-->∧

上面把添加变的操作抽取成了公共的方法！

完成！

 2141

啊！这个可能是世界上最丑的留言输入框功能~


当然，也是最丑的留言列表

有疑问发邮件到 : suibibk@qq.com 侵权立删
Copyright : 个人随笔   备案号 : 粤ICP备18099399号-2