在一些分布式系统中(如分布式缓存),我们常常使用一致性哈希[1](如哈希环)来进行数据分片。集群中的任何一台机器、集群外的客户端机器,在具备集群视图(集群中所有机器的信息)的情况下,可以确定性地计算出任意数据对应的分片位置,不需要中心化的元数据节点介入。
在分布式存储系统中,情况有所不同。因为一个分片需要存在于若干个副本中,以保证机器错误时数据不丢失。为了避免相互关联的错误(如一整个机架断电)导致多副本丢失,各副本需要摆放在几个物理隔离的错误域(如不同机架、不同可用区)之中。一致性哈希中难以建模错误域,不能胜任分布式存储中分片的任务。
因此,在常见的分布式存储系统中,我们需要中心化的元数据节点,来负责分片的副本摆放。集群中的机器不再有能力自行计算分片位置,而需要向元数据节点查询。中心化的副本选取可能会导致一些可扩展性问题。
Ceph 是一个为消灭了中心化的元数据节点而设计的分布式存储系统,集群中的机器需要自行根据集群视图来计算出分片位置。Ceph 需要一个分片算法来代替一致性哈希,不丢失一致性哈希优点的同时,又加入错误域等存储需要的建模——这就是我们今天的主角 CRUSH。它具有以下特点:
- 继承了一致性哈希的优点,如集群变动时数据迁移量小、查询高效等。
- 加入了对错误域的建模,允许不同尺度上的副本物理隔离。
- 加入了逐机器的权重,允许异质的机器集群。
- 加入了过载保护,数据分布更加平衡,避免单机过载。
本文将把 CRUSH 算法从 Ceph 的上下文中抽取出来,作为一个通用的分片摆放算法讲解。本文期望读者对一致性哈希、分布式存储系统有一定的了解。
注:本文基于 Ceph 作者2007年的博士学位论文[2],不代表当前 CRUSH 算法的实现。本人水平有限,如有错误烦请各位指正。
集群视图
集群视图(cluster map)是 CRUSH 要用到的一个重要数据,它包含整个集群下的所有服务器,将集群以树状结构表示。树中的各个中间层可自定义,但通常对应各个尺度的错误域,即集群的物理组织(如可用区、机柜行、机柜、机架等)。树的叶子层即为实际存储机器。
以下图片展示了一个包含机柜行、机柜、机架、单机几个层级的集群视图。
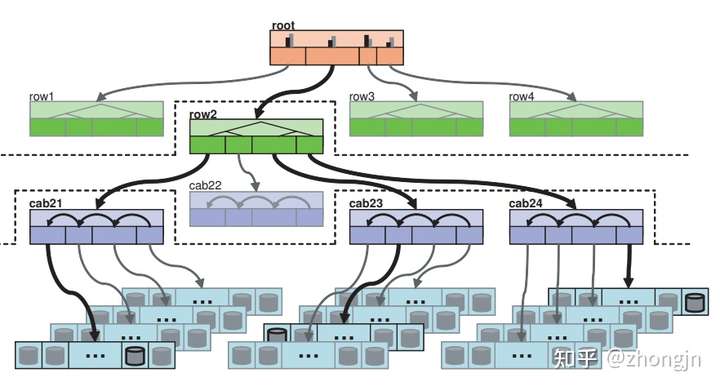
我们现在概括 CRUSH 算法:它是一个由广义的一致性哈希(不仅仅是哈希环,后面会再提到)组成的树,树中节点对应集群视图节点;机器选取即是在树中递归向下进行一致性哈希,选取子节点。这样的构造有两个关键的结果:
- 副本错误域隔离是平凡的,因为只需要在树中先选取对应数量的错误域(如3副本需要3可用区,先选取3个可用区即可)。
- 根据集群视图节点不同的变更特征、性能期望,其对应的一致性哈希不再局限于哈希环等常规实现,而是可以提供一致性哈希设计空间中更为激进的点,由用户自行选取。在节点种类章节详细介绍。
节点种类
中间节点可以具备不同的种类(bucket type),配备了不同的一致性哈希算法用来选取子节点。它们可以应对不同的变更特征、性能期望。想象两个几乎相反的情况:
- 机架是单机的父节点,机架中往往不会增加机器,因为大型集群中机器往往是以整个机架、整个机柜的形式增加。因此,机架节点可以采用并不一致的哈希(如对机器数量取余),让查询更高效。
- 可用区变化时可用区之间的数据移动要最小化。可用区的容量往往不同。因此,可用区节点可以采用最为一致的哈希,支持权重,更高的查询开销是可以接受的。
CRUSH 提供了以下4个节点种类。其中,新增、删除列代表新增、删除子节点时数据移动情况。
| 种类 | 查询 | 新增 | 删除 | 支持权重 |
|---|---|---|---|---|
| Uniform | O(1) | 差 | 差 | 否 |
| List | O(n) | 最优 | 差 | 是 |
| Tree | O(log n) | 好 | 好 | 是 |
| Straw | O(n) | 最优 | 最优 | 是 |
Uniform
具有最简单的哈希方式,子节点下标 = 数据哈希 % 子节点数量。并不一致,因为在子节点变化时数据将全部重新排布,数据移动量很大。查询高效。适合机架这种子节点(单机)很难变化的节点。
List
比较巧妙,从 算法衍生而来,子节点类似于单链表的组织,新增的子节点成为链表头部。对新增一致,对(随机)删除不一致。
查询时,从链表头开始,根据当前子节点权重计算的数据归属概率 ,随机(根据数据、节点 ID 的哈希值,具有确定性)决定是否让数据归属于当前节点;如果不归属,则递归向后查询。
在新增子节点时,子节点根据权重获得数据归属概率 。所有数据都将以
的概率转移到该子节点上;不归属的剩余数据不发生任何移动,因为算法将递归向后运行,且链表头后的链表与原链表一致。因此,List 类型的节点对新增子节点操作是一致的,数据量移动量小;但对于删除子节点则不是,像 Uniform 类型,数据将全部重新排布。
Tree
从 算法衍生而来,子节点具有二叉树组织,各项开销比较均衡。讲起来比较复杂,感兴趣的读者请移步原文。
Straw
对于一份数据,子节点之间将进行竞争:每个子节点将随机产生一个稻草值,稻草值最大的子节点拥有该份数据。对任何子节点编辑操作都一致,但查询效率较低(我感觉是无所谓的,因为集群已经是树形组织了,子节点不会太多)。
稻草值的计算方式为,随机(根据数据、节点 ID,具有确定性)产生一个0~1的值,乘以根据权重预先计算的缩放系数。缩放系数使得权重大的子节点更可能获胜。具体缩放系数的计算需要一些概率上的分析,感兴趣的读者请移步原文。
在新增、删除子节点时,仅仅只有与当前子节点直接相关的数据会被移动。其他子节点之间不会发生数据移动。下图演示了数据 "CRUSH" 从 Rack12 迁移到 Rack10 的过程。此处的 hash 函数根据哈希值产生一个0~1之间均匀分布的数。
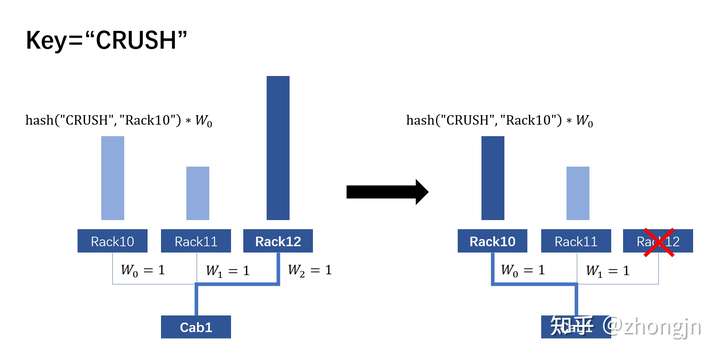
错误、过载
CRUSH 算法对于机器的错误(失效)与过载的处理依赖于集群信息变更。
对于错误的机器,它将被集群信息标记,而不是被立刻移除。因为错误往往是暂时的,机器可以在短时间内重新上线,避免数据移动。在查询(选取副本)遇到错误机器时我们需要跳过它,继续寻找合适的机器。实现的大致思路是增加目标副本数量,重新运行算法(如本来要求3副本,遇到一台机器错误时则增加为4副本,剔除掉错误机器)。
注:CRUSH 只负责寻找合适的副本摆放机器,在机器错误时 CRUSH 输出的副本摆放会发生变化;而数据层面的事情(如迁移、一致性保证)由 Ceph 中的其他组件负责,RADOS[3] 文章中有详细叙述。
对于过载的机器,它也将被集群信息标记。在查询(选取副本)遇到过载机器时,以一定概率随机(根据哈希值,具有确定性)跳过。如果决定跳过,则处理方式与上方跳过错误机器一致。